Sin Cos Tan Table - The fundamental trigonometric ratios of sin, cos, and tan are used to study the relationship between the angles and sides of a triangle, particularly a right-angled triangle. Hipparchus used the principles of trigonometry to establish the relationship between the sides and angles of a right triangle, whereas Pythagoras focused on the relationship between a right triangle's sides through the Pythagorean theorem. A right-angled triangle's missing sides or angles can be found using the trigonometry formulas sin, cos, and tan.
People also Read:
What is Sin Cos Tan in Trigonometry?
The three fundamental trigonometric ratios, namely sine, cosine, and tangent, each give the ratio of the lengths of the two sides of a right-angled triangle. We are aware that the three sides of a right-angled triangle are called the "legs" and the "hypotenuse," respectively. Thus, the longest side of a right-angled triangle is still referred to as the "hypotenuse" in trigonometry, while the other two legs are given the names:
- opposite side and
- adjacent side
Also Read: Trigonometric Ratios Table
Based on the angle we are discussing, we determine the "opposite" and "adjacent" sides.
- The side that is directly "opposite" to the angle is known as the "opposite side" or the perpendicular.
- The side that "touches" the angle (other than the hypotenuse) is referred to as the "adjacent side" or the base.

Value of Sin Cos Tan Table 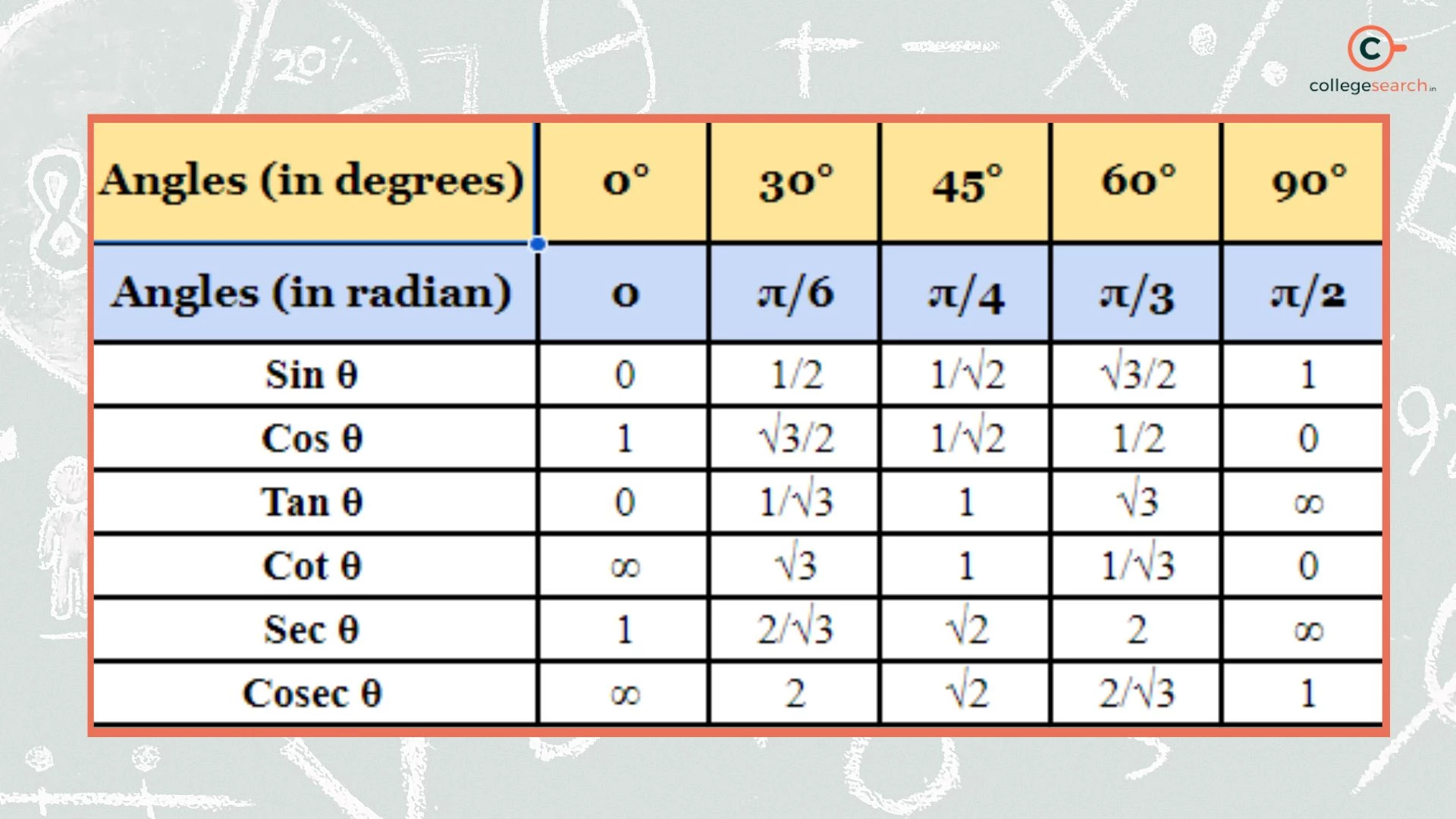
The values of the trigonometric functions are tabulated below.
Angles (in degrees) | 0° | 30° | 45° | 60° | 90° |
Angles (in radian) | 0 | π/6 | π/4 | π/3 | π/2 |
Sin θ | 0 | 1/2 | 1/√2 | √3/2 | 1 |
Cos θ | 1 | √3/2 | 1/√2 | 1/2 | 0 |
Tan θ | 0 | 1/√3 | 1 | √3 | ∞ |
Cot θ | ∞ | √3 | 1 | 1/√3 | 0 |
Sec θ | 1 | 2/√3 | √2 | 2 | ∞ |
Cosec θ | ∞ | 2 | √2 | 2/√3 | 1 |
Tips to Remember Sin Cos Tan Table
The things that you need to keep in mind from this chart are:
- The following angles are 0°, 30°, 45°, 60°, and 90°.
- The first row (of sin) can be remembered like this: 0/2, √1/2, √2/2, √3/2.
- You only need to keep that in mind because the rows of sin and cos are identical except for the order.
- Because tan equals sin/cos, each value of the tan row is obtained by dividing the corresponding values of sin by cos.
People Also Read: Upper Triangular Matrix
Practical Use
The trigonometric ratios sin, cos, and tan are frequently used in everyday life to calculate heights and distances. Sin, cos, and tan are used to solve a variety of real-world issues. Even the motions and distances of planets are calculated using it.
- Building and mountain heights, slopes, and angles of elevation are all calculated using this method.
- In the field of structural engineering, it is used to compute loads, roof slopes, flooring, etc.
- In order to determine the angle change caused by wind loads in flight aviation, trigonometry is used in flight engineering.
- Even archaeologists use it to estimate the time required for excavations.
- It is utilized in satellite systems.
- Marine engineering uses trigonometry to create marine ramps.
How to find Sin Cos Tan Values?
The steps listed below can help you remember the trigonometric values provided in the above table:
- After dividing each number by 4, find the positive roots of the following numbers: 0, 1, 2, 3, and 4.
- As a result, for angles of 0°, 30°, 45°, 60°, and 90°, we get the sine ratio values of 0, 1, 2, 1, 3, and 1.
- To find the cosine degree values for the same angles, write the sine degree values backwards.
- Because tan is the ratio of sin and cos, as in tan = sin /cos, we can determine the values of the tan ratio for the specific angles.
Sin Values
- sin 0° = √(0/4) = 0
- sin 30° = √(1/4) = ½
- sin 45° = √(2/4) = 1/√2
- sin 60° = √3/4 = √3/2
- sin 90° = √(4/4) = 1
Cos Values
- cos 0° = √(4/4) = 1
- cos 30° = √(3/4) = √3/2
- cos 45° = √(2/4) = 1/√2
- cos 60° = √(1/4) = 1/2
- cos 90° = √(0/4) = 0
Tan Values
- tan 0° = 0/1 = 0
- tan 30° = (1/2) / (√3/2) = 1/√3
- tan 45° = (1/√2) / (1/√2) = 1
- tan 60° = [(√3/2)/(½)] = √3
- tan 90° = 1/0 = ∞
Hence, the sin cos tan values are found.
Things to Remember
- To examine how a triangle's angles and sides relate to one another, use the basic trigonometric ratios Sin, Cos, and Tan.
- The formula for sin is given by the ratio of the opposite side to the hypotenuse: Sin = Opposite/Hypotenuse = tan/sec.
- The product of the sin/tan ratio and the ratio of the adjacent side to the hypotenuse is known as cos.
- Tan = Sin/Cos = Opposite / Adjacent, where Sin/Cos is the ratio of Sin to Cos, is the definition of tan.
Reciprocal Identities
A cosecant function is the sine function's reciprocal function, and vice versa. Similarly, the secant function is the cosine function's reciprocal function, and the cotangent function is the tangent function's reciprocal function.
- sin θ = 1/cosec θ
- cos θ = 1/sec θ
- tan θ = 1/cot θ
- cosec θ = 1/sin θ
- sec θ = 1/cos θ
- cot θ = 1/tan θ
Pythagorean Identities
The Pythagorean identities of trigonometric functions are as follows:
- sin2θ + cos2θ = 1
- sec2θ – tan2θ = 1
- cosec2θ – cot2θ = 1
Negative Angle Identity
The negative angle of a cosine function is always equal to the angle's positive cosine, whereas the negative angle of a sine and tangent function is equal to the angle's negative sine and tangent.
- sin (– θ) = – sin θ
- cos (– θ) = cos θ
- tan (– θ) = – tan θ
Related Article - Unit of Distance
Solved Examples
1. Evaluate sin2 30o + cos230o.
Answer:
We can deduce from the trigonometric identities that sin2
sin2 30o + cos230o = (½)2 + (√3/2)2 = ¼ + ¾
= 4/4
=> 1
2. Evaluate cos θ, If sin θ = 2/3 and tan θ < 0.
Answer:
It is understood that sin θ is positive and tan θ is negative. So θ must be in Quadrant II, where cos θ is negative. Now, sin θ = 2/3 = Opposite/Hypotenuse.
So we can assume that Opposite = 2k, Hypotenuse = 3k.
By Pythagoras theorem,
Adjacent2 = Hypotenuse2 - Opposite2
⇒ (3k)2 - (2k)2 = 5k2
Adjacent = √5k
Hence, Cos θ = - Adjacent/Hypotenuse = -√5k/3k = -√5/3
3. Evaluate sin 60°cos 30° + sin 30°cos 60°
Answer:
We all know that through trigonometric table that sin 60°= ½, cos 30°= √3/2 sin 30° = √3/2, cos 60°= ½
So, putting the values in the question, we get
½+√3/2 + √3/2+½
= 2+2√3/2